WHAT are sampling errors—and WHAT can we do about them? Part 1

Rodolfo J. Romañach,^a Aidalu Joubert Castro^a and Kim H. Esbensen^b

^aDepartment of Chemistry, University of Puerto Rico, Mayagüez Campus, Puerto Rico
^bOwner KHE Consulting, Copenhagen, Adjunct professor, Aalborg University (AAU), Denmark; Adjunct professor, Geological Survey of Denmark and Greenland (GEUS); Professeur associé, Université du Québec à Chicoutimi (UQAC), Quebec; Guest professor University of South-Eastern Norway (USN); Guest professor Recinto Universitario de Mayaguez, Puerto Rico

DOI: https://doi.org/10.1255/sew.2021.a11
© 2021 The Authors
Published under a Creative Commons BY-NC-ND licence

The objective of this column is to provide easy-to-understand examples of sampling errors. Prompted by recent participations and presentations at on-line conferences and meetings, we believe there is a need for a more fulfilling introduction and exemplification of the concept and real-world consequences of committing “sampling errors”. WHAT is a sampling error? WHAT is the result of sampling errors? WHAT can we do about sampling errors? These are welcome topics for a series of sampling columns! The point of departure will be in the Theory of Sampling and in the near infrared spectroscopy analysis and pharma application sectors, but the focus will be developed to be more general, so that readers can carry-over to other scientific and application areas of interest.

Introduction: what students in analytical chemistry learn about sampling errors

It is very instructive to start with how the topic of sampling errors is seen from the point of view of where everything ends up: analysis. What is the point of view from analytical chemistry?

At the undergraduate level, students are taught that there are seven basic steps involved in an analytical chemical analysis. These are i) method selection, ii) sample acquisition, iii) sample preparation, iv) sample analysis, v) calculation and vi) interpretation of the results… and vii) preparation of a professional report. The second step in this chemical analysis pathway is known as sampling. Sampling is defined in a frequently adopted analytical chemistry book as “the process of collecting a small mass of a material whose composition accurately represents the bulk of the material being sampled.”¹ In other words, the aliquot analysed in the lab must have the same composition as the bulk material from which it was obtained. One notes that there is no help here as to how to acquire a representative sample and a representative analytical aliquot.

Students are taught that all measurements in an analysis have an associated error, and for this reason the “true” or “exact” value can never be obtained. However, with knowledge of the different types of error and their sources, it is possible to reduce and estimate the magnitude of the error effects. Although there are many sources of analytical errors, they can traditionally be classified into three major types: systematic (or determinate) errors, random (or indeterminate) errors and gross errors.

Systematic errors

Systematic errors cause the mean of a set of analytical data to differ from the accepted value, causing all the results of a series of replicate measurements to be too high or too low. The presence of systematic errors will affect the accuracy of the analysis. Systematic errors originate from known sources or at least from sources that can be identified, and the magnitude of the systematic errors is reproducible from one measurement to another. Systematic errors can be classified into three types, according to their source: instrumental error, method errors and personal error.

Systematic-instrumental errors include, for example, changes of the original calibration, changes of the calibration due to the difference in the temperature for what it was intended for and/or changes of the glassware walls themselves during the drying process in an oven. Examples of glassware include pipets, volumetric flasks and burettes. These examples are illustrative, but not exhaustive.

Systematic-method errors are due to limitations of the analytical method itself. Reactions and reagents are examples of this type of error, i.e. they may be caused by an incomplete reaction and/or side reactions. Common examples would be lack of specificity or curtailed performance of a reagent to perform its full role in a reaction. This is, for example, the case when decomposition of an unknown sample fails to happen due to a reagent in the reaction. Thus, during a titration the extra titrant needed to produce a change in colour indicator after the equivalence point is an example of this type of error. Systematic-method errors are the most difficult to detect and correct because its correction will require a change of some, or all parts of the analytical method itself.

Systematic-personal errors are, for example, due to poor attention to important or critical aspects of the analysis context by the analyst. This may include poor judgement, carelessness and even lack of training of the analyst. Analytical bias, i.e. the tendency to skew estimates in the direction that favours the anticipated result, is considered an effect of systematic-personal errors in the analysis.²

Random errors

In analytical chemistry it is assumed that random errors cause analytical data to be scattered pretty much symmetrically around a mean value, and this error has the same probability of been positive or negative. The presence of random errors will affect the precision of the analysis. The sources of random errors are due to uncontrollable variables and because of the inability to identify their sources, they cannot be completely eliminated. A plot of relative frequency vs deviation from the mean, for a large number of individual errors, is known as a Gaussian curve or Normal Error. A Gaussian distribution assumes that only random errors are present in the analysis, i.e. that all systematic errors have been identified and corrected for. This critical assumption allows an appropriate statistical treatment of the analytical data obtained that will facilitate evaluation of the magnitude of this error—which in turn allows a bias correction to be performed.

Gross errors

Although not as common as random or systematic errors, gross errors are characterised by being “large”, which can result in an analysis being either much higher or much lower than the “true” value. The sources of gross errors are typically considered to be human errors; gross errors will manifest themselves as outliers in a series of replicate measurements.

Through the coverage of these errors in general analytical curricula, and in the relevant analytical chemistry laboratories, the need for high accuracy and precision is constantly emphasised at the undergraduate level. However, exposure to the preceding sampling process is minimal. Students are often provided with an unknown sample, but the preceding sampling step is practically always skipped.

What has been learned about sampling errors: nothing so far

Within analytical chemistry, the before analysis realm is conveniently “left out”—barring gross errors, which most definitely do not equate with the realm of sampling errors in the TOS—it is for others to take care of whatever contributions there are to the total sampling + analysis error management. Traditionally, this responsibility falls to the entity in charge of sampling in the form of more-or-less trained personnel, and the difference is critically important. For untrained personnel, sampling errors do not exist, while properly TOS-trained personnel know very well that the effects from untreated sampling errors always inflate the total analytical error budget (sampling + analytical error budget) by up to one or two orders-of-magnitude! Neglecting the effects from sampling errors is tantamount to a breach of due diligence when seen in the light of the complete “from-lot-to-aliquot” pathway.

Implications

It is, in general, not appreciated that there is both a bias issue within the analytical domain, which can be brought under complete control, however, and a sampling bias, which cannot be addressed in a similar fashion as the analytical bias can. In fact, the sampling bias cannot be corrected for by any post-analysis approach (data analytical, statistical, other). A sampling bias can only be affected by expressly eliminating all so-called “Incorrect Sampling Errors (ISE)”. ISE has been treated in various previous columns, and in the dedicated TOS literature, and will be revisited in this and later columns. But first WHAT are, and WHAT can be done about sampling errors?

Clearly, one must seek refuge within the TOS. Although often claimed to be complex, the TOS can be in fact be made accessible from a less in-depth theoretical level. For example, even though the TOS identifies nine sampling errors, they originate from only three sources: the material (which is always heterogeneous, it is only a matter of degree), the sampling equipment (which can be designed either to promote a representative extraction, or not) and the sampling process itself (even correctly designed equipment can be used in a non-representative manner).³

TOS basics on sampling errors

At the outset, the reader is referred to References 4–6. It is recommended that these are read together with, indeed before, the present column to get the best foundation for what is laid out below. Pierre Gy, founder of the TOS, took his point of departure for developing the TOS in the material phenomenon of heterogeneity—before even starting to solve the obvious main question “how to sample?” Thus, Gy identified all sampling errors that represent everything that can go wrong in sampling, sub-sampling (sample mass reduction), sample preparation and sample presentation—due to heterogeneity and/or inferior sampling equipment design and usage. He meticulously worked out how to avoid committing such practical errors in the design, manufacture, maintenance and operation of sampling equipment and elucidated how their adverse impact on the total accumulated uncertainty could be reduced as much as possible when sampling in practice. When all this was developed into his coherent TOS, the concept of a sampling error (SE) became the key element, in as much as answering the fundamental question “how to sample?” pretty much became synonymous with “how can we eliminate and/or reduce sampling error effects on sampling performance. Being able to identify sampling errors is 90 % of the way towards representative sampling. These sampling errors also occur in process analytical technologies (PAT) applications as discussed in depth in previous publications.^7,8

A crucial distinction: error vs uncertainty

Two issues underlie everything regarding “representativity”, the second of which is intimately connected with sampling errors—but, first, a related fundamental prerequisite in the TOS.

It is not possible to ascertain the representativity status of a specific sample or analytical aliquot from any observable feature related to the sample/aliquot itself. The sample could be representative, or it could be miles away—one will never know if the sample is removed from its origin. It is only possible to define, and document, representativity as a characteristic of the sampling process.⁹ Everything depends on the sampling equipment, how it is designed, used and maintained. This is where representativity can be forfeited. This is all related to which sampling errors have not been suitably eliminated and/or reduced, i.e. how one is able to recognise and how one is able to counteract sampling error effects in the sampling process. This is where and why sampling errors attain key prominence. One can state that analytical results depend on the preceding sampling and sub-sampling processes: only bona fide representative sampling/sub-sampling processes lead to a representative analytical aliquot (“the process of collecting a small mass of a material whose composition accurately represents the bulk of the material being sampled”), while anything else will leave the aliquot affected by a significant sampling bias ... of unknown magnitude (it cannot be estimated, as it changes its magnitude with every attempt to quantify it). Accuracy w.r.t. the original material from which a primary sample was extracted will be unobtainable. Clearly, focus is critically on sampling errors (“incorrect” as well as “correct”); for a more fully developed introduction the reader is referred to Esbensen’s introductory book.³ Here, focus will be on illustrating a first set of sampling error distinctions that will start one along a path to deeper understanding.

It is necessary to speak with the outmost clarity: a crucial distinction needs to be made: uncertainty vs error (Gy,¹⁰ Pitard¹¹).

Error: Difference between an observed or calculated value and the corresponding “true value”; variations in measurements (e.g. analytical results), observations or calculations which are due to mistakes or to uncontrollable factors. Sampling errors are not called sampling uncertainties!

Uncertainty: Lack of sureness about someone or something; something that is not known beyond doubt; something not constant. Without a certain amount of relevant competence (in the TOS), one would likely first listen to statisticians, who prefer the term uncertainty.

However, Pierre Gy has the following to say: “With the exception of homogenous materials, which only exist in theory, the sampling of particulate materials is always an aleatory (accidental, happening by chance, unintentional, unexpected) operation. There is always uncertainty, regardless of how small, between the true, unknown content of a lot a_L and the true unknown content of the sample a_S. A vocabulary difficulty needs to be mentioned: tradition has established the word error as common practice, though it implies a mistake that could have been prevented, while statisticians prefer the word uncertainty which implies no responsibility. However, in practice, as demonstrated in the TOS, there are both sampling errors and sampling uncertainties. Sampling errors can easily be preventatively minimised, while sampling uncertainty for a pre-selected sampling protocol is inevitable. For the sake of simplicity, and because the word uncertainty is not strong enough, the word error been selected as current usage in the TOS, making it very clear it does not necessarily imply a sense of culpability.”

With this error definition, here we are especially focused on the so-called ISEs, which are IDE, IEE, IPE and IWE, see Figure 1. They will receive the illustrative focus in this column.

IDE: Increment Delineation Error
IEE: Increment Extraction Error
IWE: Increment Weighing Error
IPE: Increment Preparation Error

The overarching thing to know about ISE forms the backbone of all practical sampling: if ISEs have not been appropriately eliminated/reduced, the sampling process is biased. All manner of bad things follow from a biased sampling process, the most important of which is that the ensuing analytical aliquot can never be representative of the target material, i.e. the game is lost even before one starts! What is the meaning of analysing an aliquot that cannot be proven to be representative? None—there is no meaning!

The first part on any sampling agenda is, therefore, to eliminate/reduce sufficiently all ISE, and in order to be able to do so, it is imperative to know how to correctly identify sampling errors a.o.

Sampling errors: WHAT are they?

For definition and full theoretical treatment of all the nine SEs, the reader is referred to the scholarly treatises by Gy¹⁰ or Pitard.¹¹ Here we shall only, and simply, illustrate these definitions and show their effects in practice….³ Many of these are particularly easy to appreciate in the process sampling realm, see Figure 1.

Figure 1. Left: archetypal examples of Increment Delineation Error (IDE) (also known as Incorrect Delineation Error). The TOS stipulates that the only correct (bias-free) increment delineation of a moving material is a complete across-stream slice (for example across a conveyor belt) or a complete cross-sectional volume (in the case of a moving material confined to a duct, e.g. in a pipeline or similar). Various other IDE manifestations resulting from i) grab sampling (top panel), “taking only some of the stream all of the time” (centre panel) and “unbalanced slicing” (bottom panel) are also illustrated—all contribute to a significant sampling bias. Right: real-world example of a highly unacceptable conveyor belt “sampling”, resulting in a highly significant IDE, here accompanied by a concomitant IEE, in that the depth of the IDE-affected slice does not extract material all the way to the bottom of the conveyor belt either. IDE and IEE are very often bad fellow-travellers towards a significant sampling bias. Illustration copyright by KHE Consulting, reproduced with permission.

Examples of sampling errors in pharma

The drying of a pharmaceutical formulation provides an example of committing a sampling error¹³ in a complex industrial production context, Figure 2.

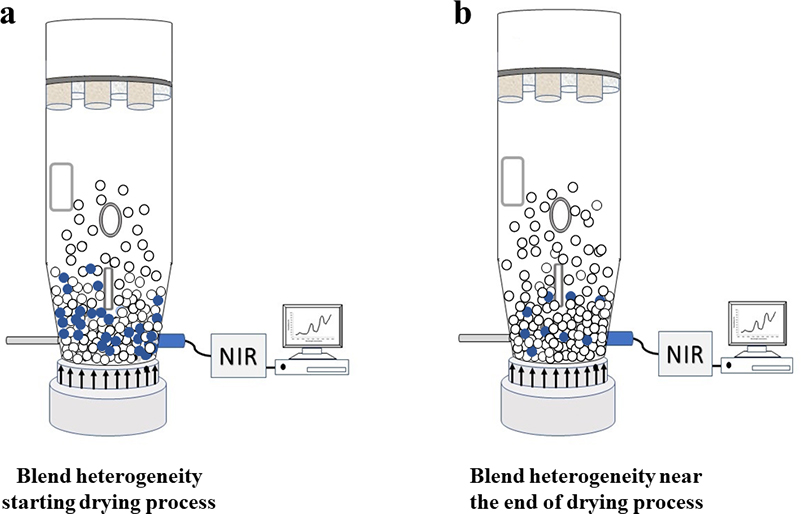
Figure 2. A fixed probe location is not necessarily always the right basis for an otherwise well-performing analytical method, e.g. a NIR probe installed close to the bottom of a drying rig. The relevance of the analytical results will vary with the compositional evolution of a drying pharmaceutical mixture. With respect to the analyte water content (moisture), segregation heterogeneity will influence the accuracy (will create a sampling bias) with respect to the full mixture volume, see text for details.

As the drying process starts, the blend is expected to have about 25 % (w/w) water content. However, a NIR spectroscopic method might indicate results of 54, 31 and 27 % (w/w), much higher than the expected level. Figure 2a provides a representative illustration of this situation where the material with the highest water content is located close to the bottom of the drying rig, i.e. close to where the NIR probe is installed. The higher results are related to the high heterogeneity of the blend at this drying stage. Figure 2b illustrates the blend near the end of the drying process, where the remaining water is more evenly distributed throughout the full volume of the dryer vessel. The same NIR probe installation now provides much more accurate results because the blend is very close to the target 4 % (w/w) water content. The volume/mass analysed by the NIR spectrometer is now less heterogeneous and the analytical probe’s GSE sampling error is reduced (GSE is a “Correct Sampling Error”, see, e.g., Reference 3).

The distribution of a drug throughout a tablet can lead to a similar heterogeneity-induced sampling error. A tablet could be manufactured in a process with a target concentration of 10 % (w/w). However, the top part of the tablet could have more drug than the bottom part of the tablet.

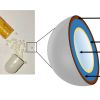
Figure 3 provides an illustration of this situation. A diffuse reflectance NIR spectroscopic approach where the sensor radiation interacts mostly with the top 1 mm of the tablet could, for example, indicate a 12 % (w/w) drug concentration. However, when the tablet is reference analysed (high performance liquid chromatography, an approach where the entire tablet is dissolved and analysed), the drug concentration is found to comply with the target concentration of 10 % (w/w). This is an example of a classical IDE—but performed by the probe—in combination with heterogeneity even at the smallest scale of interest in pharma, the scale of a single tablet. Thus, many researchers and industrial monitoring engineers/technicians prefer to develop transmission NIR methods for tablets that cover the entire tablet volume, instead of diffuse reflectance methods.

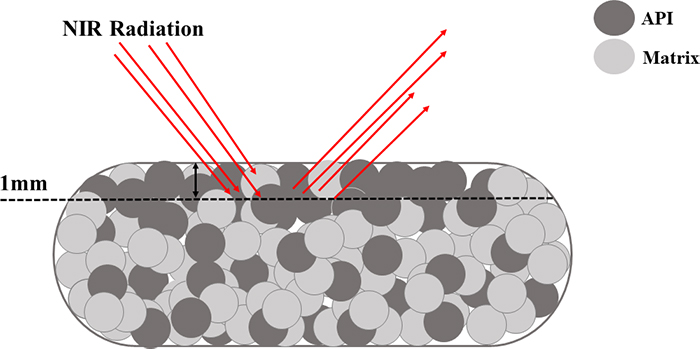
Figure 3. The inability of the diffuse NIR analytical method to penetrate more than, say, 1 mm of a single tablet, constitutes what could be called a Probe Increment Delineation Error; cf. Figure 1 for a complete slice, or a complete volume support for the signal acquisition.

For PAT analysts and chemometricians especially

A Support Mismatch Error (SME) is possible, typically when developing calibration models for PAT applications. As an example, Raman spectra may be obtained to characterise a mammalian cell culture in an active bioreactor, with the objective of developing a partial least squares (PLS) regression model to predict the concentration of key metabolites.¹⁴ Raman spectra obtained from a sample would be the X block needed for the PLS modelling. So, this application requires extracting a sample of the cell culture from the bioreactor and using it for both X-data acquisition as well as reference analysing it off-line for the metabolites, the latter which would constitute the pertinent Y data. Needless to say, this sample better be representative of the whole reactor volume (the classical TOS challenge). A significant SME will be committed if the Raman spectra are not obtained for the same sample volume which is analysed by the off-line reference method, i.e. if the support volume for the X- and the Y-data acquisition are not identical, Figure 4.

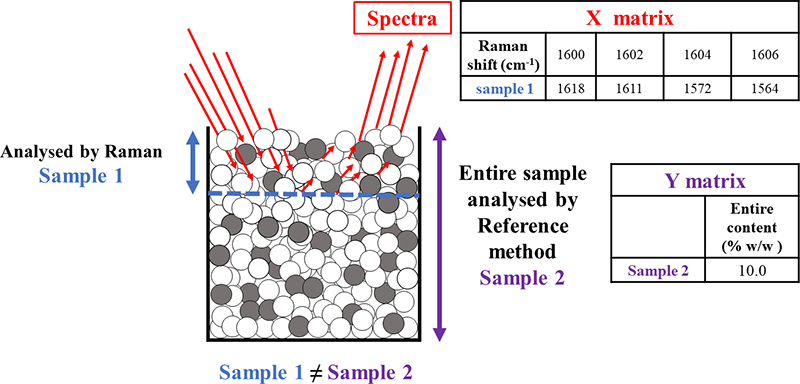
Figure 4. Focusing on the chemometric calibration modelling, may unwittingly lead to committing a SME because “sample 1”, which is analysed by Raman spectroscopy, is not supported by the same sample volume that is analysed by the reference method “sample 2”.

The data analytical correlation between the X and Y data blocks will be negatively affected by such SMEs, which sadly cannot be improved by any spectral pre-processing—or fancy regression modelling.^15,16 The fact that bioreactors are usually forcefully mixed while the Raman spectra are obtained contributes towards reducing this kind of sampling error by reducing the spatial heterogeneity of the cell culture medium in the overall reactor volume, but it cannot eliminate this entirely. Mixing or homogenisation is specified by the TOS as one of the Sampling Unit Operations that should be used to reduce sampling error effects from of heterogeneity,^3,16 and this should of course be used liberally. But the fundamental mismatch between the physical analytical volumes (masses) characterised by the two different analytical modalities is a structural condition that must be rectified in order to be able to decrease the pertinent root mean square error of prediction of the chemometric prediction model applied. The TOS insight helps us to understand why re-design of the [X,Y] data acquisition set-up can at times be less costly than carrying around an unnecessary load of ISEs. Much more on ISE, and their counterparts (the so-called “Correct Sampling Errors”, CSE) in future sampling columns.

Discussion and conclusions

In the drying example, the NIR method is detecting areas of the blend that have a high water-concentration since the drying process is just starting. If the sample analysed by the NIR radiation could be pulled out and analysed by a Karl Fischer titration (the same physical sample volume), the analytical result obtained would be similar though. However, both results are not representative of the whole blend. The samples analysed do not refer to a complete slice of the drying rig, far less to the entire drying vessel volume, but refer to a small volume directly in front of the sensor probe only, a volume with excess water. The sensor is in fact performing probe grab sampling, a classical TOS error.³ If the analyst does not realise that high water content heterogeneity is affecting the analytical results, a significant amount of time would be spent in troubleshooting an analytical method that in fact works perfectly correctly. Understanding how heterogeneity affects the manifestation of sampling errors, and what will ensue if sampling errors are not properly counteracted, is very helpful. The TOS is needed even within the analytical realm.

The NIR method s.s. also correctly determines the 12 % (w/w) drug concentration in the restricted top-most area of the tablet analysed. The spectrum obtained does indeed correspond to this concentration. The problem is not the NIR method; the problem is the heterogeneity of the tablet. The problem could be corrected, for example, by obtaining spectra of both sides of the tablet, which would detect the differences in drug concentration throughout the tablet. The problem could also be corrected by developing a NIR transmission method which would analyse the majority/all of the tablet mass, again including both sides of the tablet. The problem does not require modifying the chemometric calibration model; it only requires modifying the tablet spectral acquisition setup, or what could be called the probe sampling setup.

The SME related to the bioreactor example may also be corrected. This error was discussed by Mark,¹⁷ and has been addressed in full in a recent PAT exposé.⁷ The SME confusion is in fact one of the most pervasive issues in the PAT realm. This problem is not solved through any spectroscopy or chemometric approach, i.e. by trying to find a different spectral area for the calibration model, by changing spectral pre-processing or by any PLS-model mediation, e.g. trying one or two extra PLS-components might be able to compensate—all of which are completely futile. The SME is a sampling error, pure and simple, and should be addressed exclusively as such; later columns will further illustrate these issues.

Acknowledgements

The authors thank graduate student Adriluz Sánchez Paternina for preparation of figures.

References

1. D.C. Harris, Quantitative Chemical Analysis, 9^th Edn. W.H. Freeman. New York (2015).
2. D.A. Skoog, D.M. West, F.J. Holler and S.R. Crouch, Fundamentals of Analytical Chemistry. Nelson Education (2013).
3. K.H. Esbensen, Introduction to the Theory and Practice of Sampling. IMP Open, Chichester (2020). https://doi.org/10.1255/978-1-906715-29-8
4. K. Esbensen, “Pierre Gy (1924–2015): the key concept of sampling errors”, Spectrosc. Europe 30(4), 25–28 (2018). https://doi.org/10.1255/sew.2018.a1
5. K.H. Esbensen, “Reprint: 50 years of Pierre Gy’s ‘Theory of Sampling’—WCSB1: a tribute”, TOS Forum 6(6), 4–7 (2016).
6. P. Gy, “Sampling of discrete materials - a new introduction to the theory of sampling - I. Qualitative approach”, Chemometr. Intell. Lab. Syst. 74(1), 7–24 (2004). https://doi.org/10.1016/S0169-7439(04)00167-4
7. K.H. Esbensen and P. Paasch-Mortensen, “Process sampling: Theory of Sampling – the missing link in process analytical technologies (PAT)”, in Process Analytical Technology, Ed by K. Bakeev. John Wiley & Sons, Chichester, pp. 37–80 (2010). https://doi.org/10.1002/9780470689592.ch3
8. R.J. Romañach, “Theory of Sampling - from missing link to key enabler for process analytical technology (PAT)”, in 8th World Conference on Sampling and Blending, Ed by S.C. Dominy and K.H. Esbensen. Australian Institute of Mining and Metallurgy, Perth, Australia, pp. 63–68 (2017).
9. Danish Standards Foundation, DS 3077 Representative Sampling - Horizontal Standard. Danish Standards Foundation (2013).
10. P. Gy, Sampling for Analytical Purposes, 1st Edn. Wiley, New York (1998).
11. F.F. Pitard, Theory of Sampling and Sampling Practice. CRC Press (2019). https://doi.org/10.1201/9781351105934
12. A. Sánchez-Paternina, N.O. Sierra-Vega, V. Cárdenas, R. Méndez, K.H. Esbensen and R.J. Romañach, “Variographic analysis: A new methodology for quality assurance of pharmaceutical blending processes”, Comput. Chem. Eng. 124, 109–123 (2019). https://doi.org/10.1016/j.compchemeng.2019.02.010
13. R.L. Green, G. Thurau, N.C. Pixley, A. Mateos, R.A. Reed and J.P. Higgins, “In-line monitoring of moisture content in fluid bed dryers using near-IR spectroscopy with consideration of sampling effects on method accuracy”, Anal. Chem. 77(14), 4515–4522 (2005). https://doi.org/10.1021/ac050272q
14. T.E. Matthews, B.N. Berry, J. Smelko, J. Moretto, B. Moore and K. Wiltberger, “Closed loop control of lactate concentration in mammalian cell culture by Raman spectroscopy leads to improved cell density, viability, and biopharmaceutical protein production”, Biotech. Bioeng. 113(11), 2416–2424 (2016). https://doi.org/10.1002/bit.26018
15. K.E. Esbensen and B. Swarbrick, Multivariate Data Analysis – In Practice. An Introduction to Multivariate Analysis, Process Analytical Technology and Quality by Design, 6th Edn. CAMO Software AS, Oslo, Norway (2018).
16. K.H. Esbensen, R.J. Romañach and A.D. Román-Ospino, “Theory of Sampling (TOS): A necessary and sufficient guarantee for reliable multivariate data analysis in pharmaceutical manufacturing”, in Multivariate Analysis in the Pharmaceutical Industry, Ed by A.P. Ferreira, J.C. Menezes and M. Tobyn (Eds). Academic Press, London, pp. 53–91 (2018). https://doi.org/10.1016/B978-0-12-811065-2.00005-9
17. H. Mark, Principles and Practice of Spectroscopic Calibration. Wiley (1991).

Rodolfo Romañach

Dr Rodolfo Romañach is Professor of Chemistry at the University of Puerto Rico – Mayagüez Campus, and site leader for the Center for Structured Organic Particulate Systems. He worked in the pharmaceutical industry for over 12 years before joining the UPR Chemistry Department in 1999. He found his mission in training a new generation of pharmaceutical scientists capable of doing real time process measurements in the manufacturing area. He is presently continuing efforts to improve the teaching of chemometrics and further his understanding of the errors that affect real time process measurements—and what to do about all this.
 0000-0001-7513-7261
[email protected]

Aidalu Joubert

Dr Joubert is an Associate Professor of Chemistry at the University of Puerto Rico – Mayagüez Campus. She joined the Department of Chemistry after graduating from Washington State University in 1998. From 2014 to 2016, she served as Interim Department Chair, and has since then focused her efforts on teaching several undergraduate analytical chemistry courses.
 0000-0003-3639-3566
[email protected]

Kim Esbensen

Kim Esbensen, PhD, Dr (hon) has had a career in research and academia for 40 years, and now is an independent researcher and consultant, founding KHE Consulting. A geologist/geochemist/data analyst by training, he first worked for 20+ years in the forefront of chemometrics, but since 2000 has devoted most of his efforts to representative sampling of heterogeneous materials, processes and systems, PAT and chemometrics. He is a member of several scientific societies and has published over 260 peer-reviewed papers and is the author of two widely used textbooks in Multivariate Data Analysis and Sampling.
 0000-0001-6622-5024
[email protected]