Chris Burgessa and John P. Hammondb
aBurgess Analytical Consultancy Limited, ‘Rose Rae’, The Lendings, Startforth, Barnard Castle, Co. Durham, DL12 9AB, UK
bStarna Scientific Ltd, 52–54 Fowler Road, Hainault Business Park, Hainault, Essex, IG6 3UT, UK
The performance specification of “fitness for purpose” for ultraviolet (UV) spectrometers used in regulated environments, applying documented control, e.g. pharmacopoeial monographs or internationally recognised control standards, includes the need to specify requirements for absorbance accuracy and precision. This would seem a relatively easy task, but there are a variety of ways of specifying the acceptance criteria and hence Decision Rules. These include absolute values, percentage limits, ranges of values and, for precision, standard and relative standard deviations.
The wording specifying these performance requirements should be scientifically sound, clear and unambiguous. Unfortunately, however, given the global nature of international standards, this is not always readily achievable.
Let us consider the easier one of accuracy. This is usually determined by comparative replicate measurements of a certified reference material (CRM). A typical statement of requirement might be:
The absorbance accuracy can be determined from the mean value of six replicate measurements of absorbance of a CRM. The absorbance accuracy of the mean must be ± 0.005 from the certified value (for absorbance values below 1.0 A) or ± 0.005 multiplied by A (for absorbance values above 1.0 A) and that the range of individual values must not exceed ± 0.010 from the certified value (for absorbance values below 1.0 A) or ± 0.010 multiplied by A (for absorbance values above 1.0 A).
With precision, we have two options; one based upon a standard deviation and the other on a range. Typical statements might be:
The absorbance precision can be determined from the standard deviation of six replicate measurements. This standard deviation must not exceed 0.5 % or 0.5 % multiplied by A for absorbance values above 1.0 A.
or
The absorbance precision can be determined by the range of deviations from the mean of six replicate measurements. This range must not exceed ± 0.005 absorbance units (for absorbance values below 1.0 A) or ± 0.005 multiplied by A (for absorbance values above 1.0 A).
Therefore, we can imagine a specification for absorbance accuracy and precision with four possible acceptance criteria Decision Rules (Table 1).
Table 1. Decision Rule types.
Decision Rule number | Criteria | Acceptance limits |
#1 | Mean absorbance | ± 0.005 A from the certified standard |
#2 | SD of individual absorbances | Not greater than 0.5 % |
#3 | Range of individual absorbances | ± 0.010 A |
#4 | Range of individual deviations from observed mean absorbance | ± 0.010 A |
So, will the selection of some of these criteria make a difference to the decision regarding the “fitness for purpose” of an instrument? The answer is it depends!
Assume that we have a certified reference standard with a certified absorbance value at a specified wavelength of 1.000 and we make six measurements on four different instruments. The results are shown in Table 2.
- Instrument 1 is both sufficiently accurate and precise for all four criteria, so is unambiguously “fit for purpose”.
- Instrument 2 meets three of the four criteria but fails on the range (Decision Rule 3).
- Instrument 3 meets three of the four criteria but fails on the mean (Decision Rule 1).
- Instrument 4 fails all four criteria so is unambiguously not “fit for purpose”.
Table 2. Results from six measurements on four different instruments of a CRM.
Observed absorbances | ||||
# | Instrument 1 | Instrument 2 | Instrument 3 | Instrument 4 |
1 | 1.005 | 1.010 | 1.008 | 1.007 |
2 | 0.995 | 0.999 | 0.999 | 0.989 |
3 | 0.997 | 1.002 | 1.008 | 0.992 |
4 | 1.003 | 1.008 | 1.007 | 0.999 |
5 | 1.001 | 1.006 | 1.007 | 0.988 |
6 | 0.999 | 1.004 | 1.004 | 0.986 |
Mean | 1.000 | 1.005 | 1.006 | 0.994 |
SD | 0.37 % | 0.40 % | 0.35 % | 0.80 % |
Range | 0.010 | 0.011 | 0.009 | 0.021 |
Deviations from mean absorbance | ||||
# | Instrument 1 | Instrument 2 | Instrument 3 | Instrument 4 |
1 | –0.005 | –0.005 | –0.003 | –0.014 |
2 | 0.005 | 0.006 | 0.006 | 0.004 |
3 | 0.003 | 0.003 | –0.003 | 0.001 |
4 | –0.003 | –0.003 | –0.002 | –0.005 |
5 | –0.001 | –0.001 | –0.002 | 0.005 |
6 | 0.001 | 0.001 | 0.001 | 0.007 |
From a practical point of view, a choice has to be made to select either Decision Rule 2 or Decision Rule 3. Looking at instrument 2, the standard deviation is comfortably below 0.50 % but the range is outside the acceptance criteria. Contrast this with Instrument 1, for which the range is only 0.001 lower at the upper acceptance limit.
Whilst it is easier to rely on a data range, the standard deviation Decision Rule is more forgiving, although it requires a calculation. If Instrument 2’s values were 1.010, 0.996, 1.004, 1.008, 1.006, 1.004 giving a range of 0.014, the standard deviation is still only 0.48 %.
In the above example, whilst there is clearly a discussion around which of the Decision Rules to choose, however, the acceptance criteria clearly allow a “fit for purpose” decision to be made, and therefore these acceptance criteria, whilst they may be described as challenging, do fulfil the role for which they were intended, i.e. they establish effective control of a system.
This analysis of a simple set of measurements shows that various Decision Rules can be applied, even in this simple scenario.
If one now considers absorbance accuracy data as a set of measurement results from a CRM, with the intention of using this data “as evidence of control” in the qualification of an instrument system, the analysis takes on another level of sophistication with respect to the ISO-based Decision Rule(s).1
These rules give a prescription for the acceptance or rejection of a product based on the measurement result, its uncertainty and the specification limit or limits, taking into account the metrological uncertainty. This includes an acceptable level of the probability of making a wrong decision.2
Based on these Decision Rules, an “acceptance zone” and a “rejection zone” are determined, such that if the measurement result lies in the acceptance zone the system is declared compliant and if in the rejection zone it is declared non-compliant.
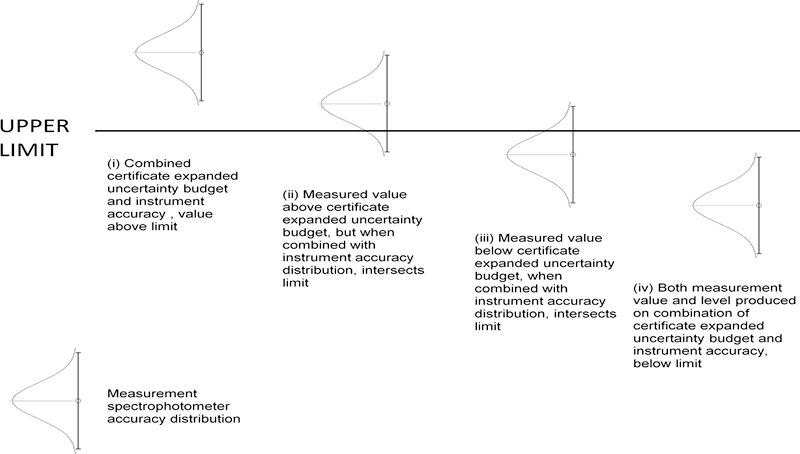
Figure 1. Assessment of Compliance with Upper Limit (CRM certified value + measurement spectrometer accuracy).2
Figure 1 shows typical scenarios arising when measurement results from a CRM are used to assess compliance with an upper specification limit, as defined above. The vertical lines show the expanded uncertainty ± U on each result and the associated curve indicates the inferred probability density function for the value of the measurand (measured value of the CRM on the spectrophotometer under test), showing that there is a larger probability of the value of the measurand lying near the centre of the expanded uncertainty interval than near the ends.
Cases i) and iv) are reasonably clear; the measurement results and their uncertainties provide good evidence that the value of the measurand is well above or well below the limit, respectively. In the case of (ii), there is a probability that the value of the measurand is above the limit, but the limit is nonetheless within the expanded uncertainty interval. Similarly, in case (iii), the distribution intersects the limit, and there is an increased probability that the value of the measurand is within the specification limit.
In a previous article,3 the authors discussed “Is your Spectrometer in Calibration” and described the use and applicability of the above Decision Rule based on the simple linear addition of the Expanded Uncertainty Budget of the CRM to the accuracy specification of the spectrometer “under test”.
Now consider the following accuracy statement, and the analysis thereof, using this generally accepted Decision Rule.
In the absorbance range encompassing 0.2 to 0.8, the photometric accuracy shall not differ by more than ± 0.5 % of samples whose absorbance has been established by a standardising laboratory.4
Whilst the use of “0.5 %” may at first glance seem “similar” to the above discussed accuracy example, however, closer examination reveals the following.
Within the stated 0.2–0.8 A range, if you calculate the 0.5 % tolerance then you produce the results shown in Table 3.
Table 3. Calculated absolute absorbance (A) limits.
Measured absorbance (A) | 0.5 % tolerance (A) |
0.2000 | 0.0010 |
0.3000 | 0.0015 |
0.4000 | 0.0020 |
0.5000 | 0.0025 |
0.6000 | 0.0030 |
0.7000 | 0.0035 |
0.8000 | 0.0040 |
Given the above requirement, in absorbance terms, let us consider various scenarios, and the associated possible Decision Rules.
Scenario #1
Criteria: In absolute absorbance values the above statement now becomes:
In the absorbance range encompassing 0.2 to 0.8, the photometric accuracy of a reference material established by a standardising laboratory shall certify a value in this range with a tolerance of ± 0.001 A at the 0.2 A level, and ± 0.004 A at 0.8 A.
There are photometric accuracy materials that have certified expanded uncertainty budgets, i.e. NIST primary standard reference materials (SRMs) and secondary CRMs from ISO/IEC 17025 certified organisations which lie within this range. But, with respective budgets of 0.0023 A and 0.0027 A, even these high-quality CRMs cannot meet the lower end of the range requirement below these values.
Scenario #2
In the absorbance range encompassing 0.2 to 0.8, the photometric accuracy shall not differ by more than ± 0.5 % of samples whose absorbance has been established by a standardising laboratory.
Criteria: This statement relates to a system “under test” and not just specifically referring to the limits associated with the reference material.
Now the required levels cannot be achieved, as already stated, by use of the uncertainty budget associated with the CRM, or by the specification of a good quality laboratory UV/vis spectrometer even when considered individually. Apply the Decision Rule where they also have to be combined in a linear manner and clearly you have a problem.
For example:
A double-beam, double-monochromator has a typical specification of ± 0.0015 A.
A single monochromator instrument typically has a specification of ± 0.003 to 0.005 A.
The “best measurement” capability of NIST in the above range was produced by their certification of SRM 930e, at ± 0.0023 A.5
So, adding these values together we get 0.0038 A “at best”, and typically 0.0053 A to 0.0073 A.
Clearly, in both above scenarios, compliance with the requirement cannot be achieved with the Decision Rules stated, so the question must be:
“…what Decision Rule is expected to be applied and, given the above discussion, how is it expected that an accuracy of ± 0.001 A at the 0.2 A be achieved?”
In addition, which UV spectrometer are you going to use to achieve such measurement performance when the requirement is better than the best measurement capability of national laboratories?
References
- ISO 14253-1:1998 Geometrical Product Specifications (GPS)—Inspection by Measurement of Work Pieces and Measuring Equipment—Part 1: Decision Rules for Proving Conformance or Non-Conformance with Specifications. ISO, Geneva (1998). https://www.iso.org/standard/23021.html
- S.L.R. Ellison and A. Williams (Eds), EURACHEM/CITAC Guide “Use of Uncertainty Information in Compliance Assessment”, 1st Edn. Eurachem, Torino (2007). https://www.eurachem.org/index.php/publications/guides/uncertcompliance
- C. Burgess and J.P. Hammond, “Is your spectrometer in compliance”, Spectrosc. Europe 28(2), 16–17 (2016). https://www.spectroscopyeurope.com/quality/your-spectrometer-calibration
- Standard Test Method for Naphthalene Hydrocarbons in Aviation Turbine Fuels by Ultraviolet Spectrophotometry. D 1840-07, ASTM International (2014). https://www.astm.org/Standards/D1840.htm
- Certification for SRM 930e, Neutral Density Glass Filters. National Institute of Standards and Technology (NIST), USA. https://www-s.nist.gov/srmors/certificates/archives/930e.pdf














This is really informative
This is really informative article